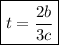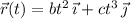
The velocity at time
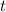 is
is
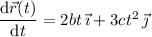
Take two vectors that point in the positive
 and positive
and positive
 directions, such as
directions, such as
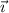 and
and
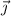 . The dot products of the velocity vector with
. The dot products of the velocity vector with
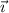 and
and
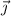 are
are
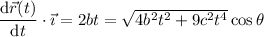
and
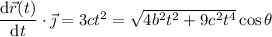
We want the angles between these vectors to be 45º, for which we have
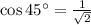 . So
. So
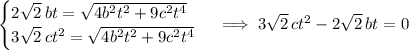
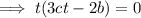
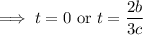
When
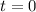 , the velocity vector is equal to the zero vector, which technically has no direction/doesn't make an angle with any other vector. So the only time this happens is for
, the velocity vector is equal to the zero vector, which technically has no direction/doesn't make an angle with any other vector. So the only time this happens is for