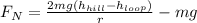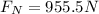Question

A roller coaster car starts from rest at the top of a hill 15 m high and rolls down to ground level. From there it starts into a vertical loop. Exactly at the top of the loop it is 10 m high and the radius of curvature of the track is 4.0 m. Assuming negligible friction and air resistance, what is the magnitude of the normal force acting on a 65 kg passenger at the top of the loop?

Answer 1

955.5N

Step-by-step explanation:

The normal force is given by the difference between the centripetal force and gravity at the top of the loop:

`F_N = F_C - F_G = m(v^(2) )/(r) - mg`

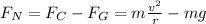
mass m = 65kg

radius of the loop r = 4m

velocity v = ?

g = 9.8 m/s²

To find the centripetal force, you need to find the velocity of the car at the top of the loop.

Use energy conservation:

`E_(tot)=mgh + (1)/(2) mv^(2)`

At the top of the hill:

`E_(tot)= mgh_(hill)`

At the top of the loop:

`E_(tot)=mgh_(loo)_p +(1)/(2) m v^(2)`

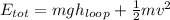
Setting both energies equal and canceling the mass m gives:

`gh_(hill) = gh_(loo)_p + (1)/(2) v^(2)`

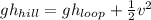
Solving for v:

`v^(2) = 2g(h_(hill)-h_(loo)_p)`

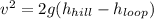
Using v in the first equation:

`F_N = (2mg(h_(hill)-h_(loo)_p))/(r) - mg`

`F_N = 955.5N`