Answer:
The length of the diagonal HJ is 10.82 units
Explanation:
* Lets revise the rule of the distance between two points
-
 , where
, where
 and
and
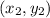 are the two points
are the two points
* Lets use this rule to find the length of the diagonal HJ
∵ The coordinates of point H are (-4 , 3)
∵ The coordinates of point J are (5 , -3)
∴
 and
and

∴
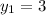 and
and

- Lets find the length of the diagonal HJ by using the rule above
∴ HJ =
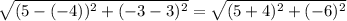
∴ HJ =
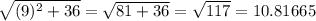
∴ HJ = 10.82
* The length of the diagonal HJ is 10.82 units