Question

A 5000-kg spacecraft is in a circular orbit 2000 km above the surface of Mars. How much work must the spacecraft engines perform to move the spacecraft to a circular orbit that is 4000 km above the surface? Assume the mars radius is 3.4 \times 10^6 m3.4×10 6 m and the mass of mars is  6.4 \times 10^{23}6.4×10 23  kg. (Express your answer in the format: 1.23 \times 10^{10} J1.23×10 10 J as "1.23e10 J".)

Answer 1

W = 0.483 x 10^10 J

Step-by-step explanation:

M = mass of mars = 6.39 x 10^23 kg

m = mass of spacecraft = 5000 kg

R = radius of mars = 3.4 x 10^6 m

hi = initial height = 2000 km = 2 x 10^6 m

hf = final height = 4000 km = 4 x 10^6 m

ri = initial distance from center of mars

ri = R + hi

`ri = 3.4 x 10^6 + 2 x 10^6 = 5.4 x 10^6 m`

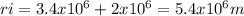
rf = final distance from center of mars

rf = R + hf

`rf = 3.4 x 10^6 + 4.00 x 10^6 = 7.4 x 10^6 m`

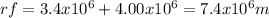
Total energy at an altitude of ''r'' is given as :;

`E = (-GMm)/(2r)`

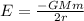
Energy at height ''ri''

`Ei = -((6.67 x 10^(-11)) (6.39 x 10^(23) ) (5000))/(2*5.4 x 10^6)`

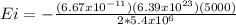
Ei = -1.973 x 10^10 J

Energy at height ''rf''

`Ef = -((6.67 *10^(-11)) (6.39 *10^(23) ) (5000))/((2*7.4 *10^6))`

Ef = - 1.439*10^10 J

work done is given as ::

W = (- 1.439*10^10 J) - (-1.973 x 10^10) J

W = 0.483 x 10^10 J