Answer:
Kₐ = 1.2 × 10⁻⁷
Step-by-step explanation:
Step 1. Calculate [H₃O⁺]
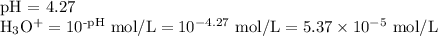
2. Calculate Kₐ
HNO₂ + H₂O ⇌ H₃O⁺ + NO₂⁻
I/mol·L⁻¹: 0.025 0 0
C/mol·L⁻¹: 0.025-5.4 × 10⁻⁵ +5.4 × 10⁻⁵ +5.4 × 10⁻⁵
E/mol·L⁻¹: 0.025 5.4 × 10⁻⁵ 5.4 × 10⁻⁵
So, at equilibrium,
[H₃O⁺] = [NO₂⁻] = 5.4 × 10⁻⁵ mol·L⁻¹
[HF] = 0.025 mol·L⁻¹
Kₐ = {[H₃O⁺][NO₂⁻]}/[HNO₂
Kₐ = (5.4 × 10⁻⁵ × 5.4 × 10⁻⁵)/0.025
Kₐ = 2.9 × 10⁻⁹/0.025
Kₐ = 1.2 × 10⁻⁷
The acid is not nitrous acid, because the Kₐ of HNO₂ is 7.2 × 10⁻⁴