Answer:
c) 335 Hz
Step-by-step explanation:
Given that the two sources:
S₁ ≡ (0 m, 2 m)
S₂ ≡ (-2 m, 0 m)
The lady hears the destructive interference for the first time when she reaches the point (0.6 m, 0 m).
So, the path difference = Δx = |S₂P - S₁P|
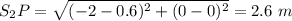
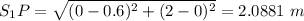
So,
Δx = |2.6 - 2.0881| = 0.5119 m
For, first destructive interference, Δx = λ / 2
So,
Wavelength = 1.0238 m
Also,
c = ν×λ
Where,
c is the speed of sound wave having value as 346 m/s
ν is the frequency
λ is the wavelength
So,
ν = c / λ = 346 m/s / 1.0238 m ≈ 335 Hz