Answer: 0.0129
Explanation:
Given : Sample size : n=32
The average amount of time spent texting over a one-month period is :
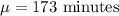
Standard deviation :
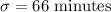
We assume that the time spent texting over a one-month period is normally distributed.
z-score :
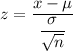
For x= 199

Now by using standard normal table, the probability that the average amount of time spent using text messages is more than 199 minutes will be :-
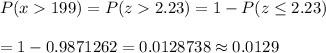
Hence, the required probability = 0.0129