Question

(20 pts!) if the base of the roof has length 40 feet and x=30, which of the following gives the height of the roof?

Answer 1

40/√3 feet

Explanation:

Given,

Base of the roof,b=40 feet

Base angle,x=30°

Formula to calculate length of the roof,l=

`(b)/( \cos(x) )`

or,l=40/cos(30°)

or,l=40*(√3/2)

or,l=80/√3

Now,In the above triangle, using Pythagoras formula,

hypotenuse^2=base^2+height^2

If total height be h,

h^2+b^2=l^2

or,h^2=l^2-b^2

or,h^2=(80/√3)^2-40^2

or,h^2=6400/3 - 1600

or,h^2=1600/3

or,h=40/√3

ANS:40/√3 feet

Answer 2

23.094 ft approximately

(If you want your answer in a different format, let me know please.)

Explanation:

I would have solve this using tangent since the side opposite to x is asked for and the adjacent side to side is given as having a measurement of 40 ft.

But I think they want you to use the formula:

`l=(b)/(\cos(x))`.

`l=(40)/(\cos(30))`

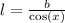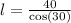
Input into calculator:

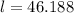`l=46.188` (approximation)

l represents the length of the roof.

So we have l=46.188 and b=40.

We must use the Pythagorean Theorem to find the height,h, for of the roof.

l is the hypotenuse.

`h^2+40^2=46.188^2`

`h^2+1600=2133.331`

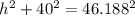
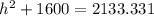
Subtract 1600 on both sides:

`h^2=533.331`

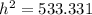
Take square root of both sides:

`h=23.094`

The answer is 23.094 feet for the height that roof reaches on the building.

I want to show you another way:

`\tan(x)=\frac{\text{opposite}}{\text{adjacent}}`

`\tan(30)=(h)/(40)`

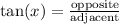
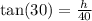
Multiply both sides by 40:

`40\tan(30)=h`

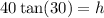
Input into calculator:

`23.094=h`

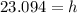
I didn't do it this way because your problem suggested you use their formula to find the height.