Question

What force (in N) does a trampoline have to apply to a 46.0 kg gymnast to accelerate her straight up at 5.30 m/s2? Note that the answer is independent of the velocity of the gymnast—she can be moving either up or down, or be stationary. (Enter the magnitude.)

Answer 1

The force acting on the trampoline is 694.6 N.

Step-by-step explanation:

It is given that,

Mass of gymnast, m = 46 kg

Acceleration of the gymnast,
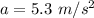`a=5.3\ m/s^2` (upward direction)

Let
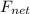`F_(net)` is the net force acting on the trampoline, F is the force exerted by the trampoline mg is the weight force acting due to gravity. As the gymnast is accelerating up, so,

`F_(net)=F-mg`

`ma=F-mg`

`F=mg+ma`

`F=m(g+a)`

`F=46* (9.8+5.3)`

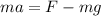
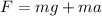
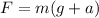
F = 694.6 N

So, the force acting on the trampoline is 694.6 N. Hence, this is the required solution.

Answer 2

So draw a free body diagram. Let the top be the increasing direction for y and let the bottom be the decreasing direction. All other coordinates are trivial for the problem. You will notice that during the time of impact with the trampoline, there are two forces in the y direction, the weight of the gymnast and the force exerted by the trampoline. The y component of the total force is:

`F_(y)=F_(T)-mg`

where F_T is the force exerted by the trampoline. According to Newton's Second Law, we have the differential equation:

`F_(y)=m\ddot{y}=F_(T)-mg`

Dividing both sides by m we get:

`\ddot{y}=(F_(T))/(m)-g`

which is the acceleration in the y direction. Now solving for F_T we get:

`F_(T)=m(\ddot{y}+g)`

Now plugging in m=46.0 kg, the acceleration in the y=5.30 m/s^2 and g=9.8 m/s^2, we get

`\[F_(T)=694.6 N\]` if I am not mistaken.

Hope this helped.