Answer:
Two questions:
Question 1:
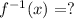 given
given
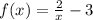 .
.
Answer 1:
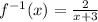
Question 2:
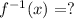 given
given
 .
.
Answer 2:
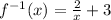
Explanation:
So
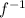 is used in most classes to represent the inverse function of
is used in most classes to represent the inverse function of
 .
.
The inverse when graphed is a reflection through the y=x line. The ordered pairs
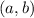 on
on
 implies
implies
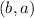 are on
are on
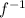 .
.
This means we really just need to swap x and y.
Since we want to write as a function of x we will need to solve for y again.
Question 1:
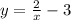
Swap x and y:
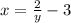
We want to solve for y.
Add 3 on both sides:
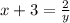
Make the left hand side a fraction so we can cross-multiply:
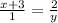
Cross multiply:
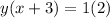
Simplify right hand side:
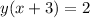
Divide both sides by (x+3):
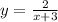
So
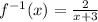 .
.
Question 2:
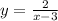
Swap x and y:
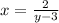
Make left hand side a fraction so we can cross multiply:
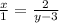
Cross multiply:
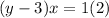
We have to distribute here:
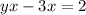
Add 3x on both sides:
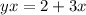
Divide boht sides by x:
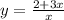
You could probably stop here but you could also simplify a little.
Separate the fraction into two terms since you have 2 terms on top bottom being dividing by x:
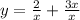
Simplify second fraction x/x=1:
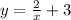
So
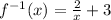 .
.