Question

A line contains the points (-3, 4) and (7, -1). Calculate the equation of the line in the form

y = mx + b

Explain each step. PS How can I draw the graph?​

Answer 1

`y=-(1)/(2)x+(5)/(2)`

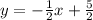
Explanation:

First we need to find the slope of the line. We can plug in both coordinates in to the slope formula.

The slope formula is:

`m=(y2-y1)/(x2-x1)`

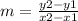
So I will use (-3,4) as the first coordinate, and (7,-1) as the second coordinate.

x₁ = -3

y₁ = 4

x₂ = 7

y₂= -1

I will plug in these values to find the slope.

`m=(y2-y1)/(x2-x1)\\\\m=(-1-4)/(7-(-3))\\\\m=(-5)/(10)\\\\m=-(1)/(2)`

Now that we know the slope is -1/2, we can plug in the slope and a point into the point slope equation. Then we can solve for y.

`y-y_(1) =m(x-x_(1) )\\\\y-4==-(1)/(2)(x-(-3))\\\\y-4=-(1)/(2)x-(3)/(2)\\\\ y=-(1)/(2)x+(5)/(2)`

I have attached an image of what this graph should look like. Since the slope is -1/2, the y value should decrease by 1/2 every time you move over by 1 on the x axis. And since the equation says "+5/2" we know we have to shift the graph up by 5/2. The y-intercept will be 5/2.

I added another image that shows how to graph an equation using the equation y=mx+b