Answer:
Given:You sample 160 men, and 25% own cats
You sample 120 women, and 20% own cats.
To Find : Find the test statistic, rounded to two decimal places.
Solution:
You sample 160 men, and 25% own cats.
No. of men have cats =
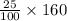
=
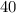
So,
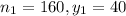
You sample 120 women, and 20% own cats.
No. of women have cats =
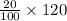
=
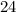
So,
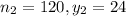
We will use Comparing Two Proportions

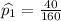
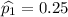
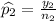
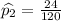
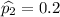
Let
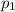 and
and
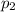 be the probabilities of men having cat and women having cat receptively
be the probabilities of men having cat and women having cat receptively
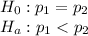
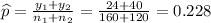
Formula of test statistic :
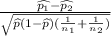
Substitute the values
test statistic :

test statistic :
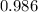
So, test statistic is 0.986