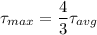Question

Determine an equation for shear-stress distribution over the cross section of a rod that has a radius c. By what factor is the maximum shear stress greater than the average shear stress acting over the cross section?

Answer 1

`\tau _(max)=(4)/(3)\tau _(avg)`

Step-by-step explanation:

Lets take

d= diameter of rod

T=Applied torque on the rod

τ=Shear stress on the rod

We know that shear stress in the rod is varying with radius r of the rod.Shear stress is zero at center of the rod and maximum at the outer most section of the rod.

From Torque-Stress

`(T)/(J)=(\tau )/(r)`

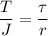
So we can say that shear stress is varying linearly with radius of rod.

We know that
`J=(\pi d^4)/(32)`

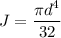
And for maximum shear stress r=R

So we can say that shear stress due to torque

`\tau _(max)=(16T)/(\pi d^3)`

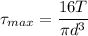
If we consider that only shear force acting on the rod then maximum shear stress is 4/3 times more than average shear stress.

`\tau _(max)=(4)/(3)\tau _(avg)`