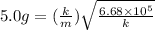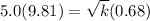Question

What should be the spring constant k of a spring designed to bring a 1200 kg car to rest from a speed of 85 km/h so that the occupants undergo a maximum acceleration of 5.0g?

Answer 1

k = 5178.8 N/m

Step-by-step explanation:

As we know that spring mass system will oscillate at angular frequency given as

`\omega = \sqrt{(k)/(m)}`

now we have

`\omega = \sqrt{(k)/(1200)}`

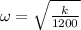
now the maximum acceleration of the spring block system is at its maximum compression state which is given as

`a = \omega^2 A`

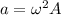
here A= maximum compression of the spring

so here in order to find maximum compression of the spring we will use energy conservation as we know that initial total kinetic energy of the car will convert into spring potential energy

`(1)/(2)mv^2 = (1)/(2)kA^2`

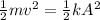
here we know that

v = 85 km/h

`v = 85 *(1000)/(3600) = 23.61 m/s`

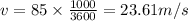
now we have

`(1200)(23.61^2) = kA^2`

`A^2 = (6.68 * 10^5)/(k)`

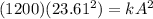
now from above equation of acceleration we have

`5.0 g = ((k)/(m))\sqrt{(6.68 * 10^5)/(k)}`

`5.0(9.81) = √(k)(0.68)`

`k = 5178.8 N/m`