Question

A company has determined that when x hundred dulcimers are​ built, the average cost per dulcimer can be estimated by ​C(x)=0.2x^2-0.6x+2.250​, where​ C(x) is in hundreds of dollars. What is the minimum average cost per dulcimer and how many dulcimers should be built to achieve that​ minimum?

Answer 1

Answer: The minimum average cost per dulcimer = $ 180

The number of dulcimers should be built to achieve that​ minimum =150

Explanation:

Given : A company has determined that when x hundred dulcimers are​ built, the average cost per dulcimer can be estimated by

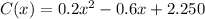`C(x)=0.2x^2-0.6x+2.250`, where​ C(x) is in hundreds of dollars.

Now, differentiate the above function with respect to x, we get

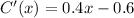`C'(x)=0.4x-0.6` (1)

Put C'(x) =0, we get

`0.4x-0.6=0\\\\\Rightarrow\ x=(0.6)/(0.4)=1.5`

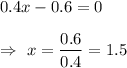
Again differentiate (1) w.r.t. x , we get

`C`

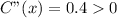
By second derivative test , we have the value of x where C(x) is minimum=1.5

`C(x)=0.2(1.5)^2-0.6(1.5)+2.250=1.8`

Hence, the minimum average cost per dulcimer = $ 180

The number of dulcimers should be built to achieve that​ minimum =150

Answer 2

The minimum average cost per dulcimer is 150 and the minimum cost is $180.

Explanation:

The given cost function is

`C(x)=0.2x^2-0.6x+2.250`

Differentiate the function C(x) with respect to x.

`C'(x)=0.2(2x)-0.6(1)+(0)`

`C'(x)=0.4x-0.6`

Equate C'(x)=0, to find the critical values.

`C'(x)=0`

`0.4x-0.6=0`

`0.4x=0.6`

Divide both sides by 0.4.

`x=(0.6)/(0.4)`

`x=1.5`

Differentiate the function C'(x) with respect to x.

`C''(x)=0.4(1)`

`C''(x)=0.4`

At x=1.5

`C''(1.5)=0.4`

The value of double derivative is positive. It means the function is minimum at x=1.5 hundred.

1.5 hundred = 150

Substitute x=1.5 in the given function to find the minimum average cost.

`C(1.5)=0.2(1.5)^2-0.6(1.5)+2.250`

`C(1.5)=1.8`

The minimum cost is 1.8 hundred dollars.

1.8 hundred dollars = $180

Therefore, the minimum average cost per dulcimer is 150 and the minimum cost is $180.