Question

Trucks in a delivery fleet travel a mean of 110 miles per day with a standard deviation of 38 miles per day. The mileage per day is distributed normally. Find the probability that a truck drives between 132 and 159 miles in a day.

Answer 1

Answer: 0.1824

Explanation:

Given : The mileage per day is distributed normally with

Mean :
`\mu=110\text{ miles per day}`

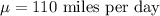
Standard deviation :
`\sigma=38\text{ miles per day}`

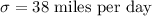
Let X be the random variable that represents the distance traveled by truck in one day .

Now, calculate the z-score :-

`z=(x-\mu)/(\sigma)`

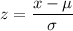
For x= 132 miles per day.

`z=(132-110)/(38)\approx0.58`

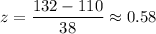
For x= 159 miles per day.

`z=(159-110)/(38)\approx1.29`

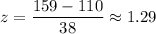
Now by using standard normal distribution table, the probability that a truck drives between 132 and 159 miles in a day will be :-

`P(132<x<159)=P(0.58<z<1.29)\\\\=P(z<1.29)-P(0.58)\\\\= 0.9014747-0.7190426=0.1824321\approx0.1824`

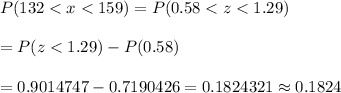
Hence, the probability that a truck drives between 132 and 159 miles in a day =0.1824