Answer: 0.1824
Explanation:
Given : The mileage per day is distributed normally with
Mean :
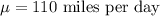
Standard deviation :
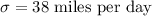
Let X be the random variable that represents the distance traveled by truck in one day .
Now, calculate the z-score :-

For x= 132 miles per day.
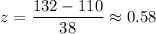
For x= 159 miles per day.
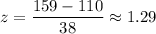
Now by using standard normal distribution table, the probability that a truck drives between 132 and 159 miles in a day will be :-
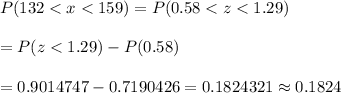
Hence, the probability that a truck drives between 132 and 159 miles in a day =0.1824