Question

Given a triangle ABC at A = ( - 1, 3 ) B = ( 1, - 1 ) C = ( 2, 2 ) and if the triangle is rotated 90 ° clockwise about the point ( 4, 1 ), find the new location of the point A'.

Answer 1

The coordinates of A' are (6,6).

Explanation:

It is given that in triangle ABC, A = (-1, 3), B = (1, - 1) and C = (2, 2).

If a point is rotated 90 ° clockwise about the point ( a,b ), then

`(x,y)\rightarrow ((y-b)+a,-(x-a)+b)`

It is given that the triangle is rotated 90 ° clockwise about the point ( 4, 1 ). So, a=4 and b=1.

`(x,y)\rightarrow ((y-1)+4,-(x-4)+1)`

`(x,y)\rightarrow (y+3,-x+5)`

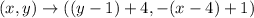
The coordinates of A are (-1,3), So, the coordinates of A' are

`A(-1,3)\rightarrow A'(3+3,-(-1)+5)`

`A(-1,3)\rightarrow A'(6,6)`

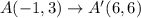
Therefore the coordinates of A' are (6,6).