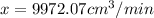Question

Water is leaking out of an inverted conical tank at a rate of 10,000 cm3/min at the same time that water is being pumped into the tank at a constant rate. The tank has height 6 m and the diameter at the top is 4 m. If the water level is rising at a rate of 20 cm/min when the height of the water is 2 m, find the rate at which water is being pumped into the tank. (Round your answer to the nearest integer.)

Answer 1

Water is being pumped at a rate of
`x=9972.07cm^(3)/min`

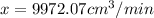
Step-by-step explanation:

We have volume of right circular cone is given by

`V=(1)/(3)\pi r^(2)h`

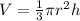
Differentiating with respect to time we get

`V=(1)/(3)\pi r^(2)h\\\\(dV)/(dt)=(\pi )/(3)(2rh* (dr)/(dt)+\pi r^(2)(dh)/(dt))`

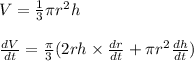
Now let the rate at which water is entering the conical vessel be
`xcm^(3)/min`

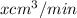
The cumulative change in volume is given by
`(10000-x)`

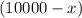
By similar angle criterion of the triangle we have

`(2)/(6)=(r(h))/(h)\\\\\therefore r(h)=(h)/(3)`

`(dr(h))/(dt)=(dh(t))/(3dt)`

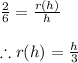
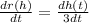
Using all the above results we in the above equation we have

`10000+x=(\pi )/(3)((2^(3)* 20)/(9)+(4* 20)/(9))`

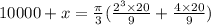
Solving for x we get

`x=9972.07cm^(3)/min`