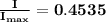Answer:
a) 7.947 radians
b)
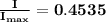
Step-by-step explanation:
y = Distance from central bright fringe = 2.5 mm
λ = Wavelength = 600 nm
L = Distance between screen and source = 2.8 m
d = Slit distance = 0.85 mm
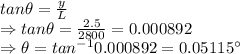
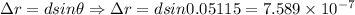
a) Phase difference
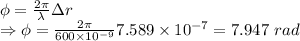
∴ Phase difference between the two interfering waves on a screen at a point 2.50 mm from the central bright fringe is 7.947 radians
b)
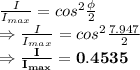
∴ Ratio of the intensity at this point to the intensity at the center of a bright fringe