Answer:
2.19 ft ( approx )
Explanation:
Let x be the width ( in ft ) of the path,
Given,
The dimension of the garden area,
Length = 30 ft, width = 20 ft,
So, the dimension of the remaining garden ( garden excluded path ),
Length = (30 - 2x) ft, width = (20-2x) ft
Thus, the area of the remaining garden,
A=(30 - 2x)(20 - 2x)
According to the question,
A = 400 ft²,
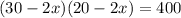
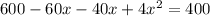


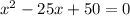
By the quadratic formula,
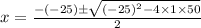

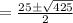
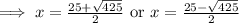
⇒ x ≈ 22.8 or x ≈ 2.19,
∵ Width of the path can not exceed 30 ft or 20 ft
Hence, the width of the path is approximately 2.19 ft.