Answer:
Resultant magnetic field =

Step-by-step explanation:
We are given that two long straight, parallel wires separated by a distance 20 cm
Le two wires A and B

Current flowing in wire=
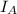 =30 A
=30 A
Current flowing in wire B=
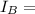 40 A
40 A
We have to find the magnitude of magnetic field at a point 15 cm from wire A and 25 cm from wire B
Magnetic field due to current

Magnetic field due to current
![I_A,B_1=[tex]10^(-7)* (2* 30)/(0.15)=4* 10^(-5)](https://img.qammunity.org/2020/formulas/physics/college/kq7bj1606kdbzidrota4i9u7012v1u91bb.png) T
T
Magnetic field due to current
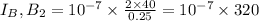 T
T
Magnetic field due to current
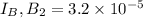
Angle between
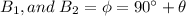
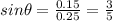
Resultant magnetic field =
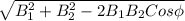
Resultant magnetic field =
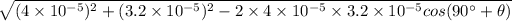
Resultant magnetic field =
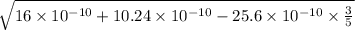
Resultant magnetic field =
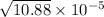
Resultant magnetic field =
