Question

An airplane climbs 100 feet during the first second after takeoff. In each succeeding second it climbs 100 feet more than it climbed during the previous second. How many seconds does it take for the plane to reach an altitude of 12,000 feet above its takeoff height?

Answer 1

Explanation:

After t seconds, the airplane's altitude (in feet) is 100 + 200 + . . . + 100t = 100(1 + 2 + . . . + t) = 100*t(t + 1)/2 = 50t(t + 1). Thus, we want to find the smallest t such that 50t(t + 1)
`\geq` 12000. Dividing both sides by 50, we get t(t + 1)
`\geq` 240. Since $15*16 = 240$, the smallest such t is t = 15.

Answer 2

15 seconds.

Explanation:

∵ The distance covered by plane in first second = 100 ft,

Also, in each succeeding second it climbs 100 feet more than it climbed during the previous second,

So, distance covered in second second = 200,

In third second = 300,

In fourth second = 400,

............, so on....

Thus, the total distance covered by plane in n seconds = 100 + 200 + 300 +400......... upto n seconds

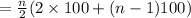`=(n)/(2)(2* 100 + (n-1)100)` ( Sum of AP )

`=(n)/(2)(200+100n-100)`

`=(n)/(2)(100+100n)`

`=50n+50n^2`

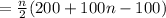
Suppose the distance covered in n seconds is 12,000 feet,

`\implies 50n+50n^2=12000`

`n+n^2=240`

`n^2+n-240=0`

`n^2+16n-15n-240=0`

`n(n+16)-15(n+16)=0`

`(n-15)(n+16)=0`

`\implies n=15\text{ or }n=-16`

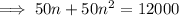
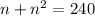
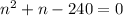
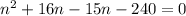
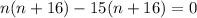
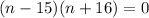
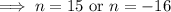
∵ n can not be negative,

Hence, after 15 seconds the plane will reach an altitude of 12,000 feet above its takeoff height.