Question

The survey included 411 adults between the ages of 55 and 64, and 50 of them said that they had used online dating. If we use this sample to estimate the proportion of all American adults ages 55 to 64 to use online dating, the standard error is 0.016. Find a 95% confidence interval for the proportion of all US adults ages 55 to 64 to use online dating.

Answer 1

Answer:
`(0.0886,\ 0.1514)`

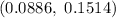
Explanation:

Given : Significance level :
`\alpha=1-0.95=0.05`

Critical value :
`z_(\alpha/2)=1.96`

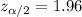
Sample size :
`n=411`

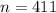
The number of adults between the ages of 55 and 64 said that they had used online dating : 54

Now, the proportion of adults between the ages of 55 and 64 said that they had used online dating :
`p=(50)/(411)\approx0.12`

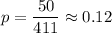
Now, the confidence interval for proportion is given by :-

`p\pm z_(\alpha/2)\sqrt{(p(1-p))/(n)}\\\\=0.12\pm(1.96)\sqrt{(0.12(1-0.12))/(411)}\\\\\approx0.12\pm 0.0314\\\\=(0.12-0.0314,\ 0.12+0.0314)\\\\=(0.0886,\ 0.1514)`

Hence, a 95% confidence interval for the proportion of all US adults ages 55 to 64 to use online dating is
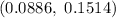`(0.0886,\ 0.1514)`.