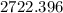Answer:
Brand 1 Brand 2 Difference
37734 35202 2532
45299 41635 3664
36240 35500 740
32100 31950 150
37210 38015 −805
48360 47800 560
38200 37810 390
33500 33215 285
Sum of difference = 2532+ 3664+740+150 −805+ 560 +390 +285 = 7516
Mean =
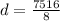
Mean =

a) d= 939.5
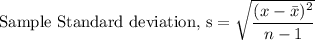
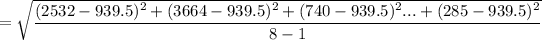
=1441.21
b)SD= 1441.21
c)Calculate a 99% two-sided confidence interval on the difference in mean life.
confidence level =99%
significance level =α= 0.01
Degree of freedom = n-1 = 8-1 =7
So,
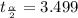
Formula for confidence interval
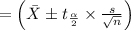
Substitute the values
confidence interval
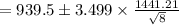
confidence interval
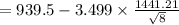 to
to

Confidence interval
 to
to