Answer:
The magnitude of the magnetic field through the center of this solenoid is 0.0568 T.
Step-by-step explanation:
Given that,
Length = 15 m
Radius r₁ = 1.6 mm
Resistivity of copper
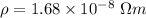
Radius
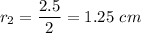
emf = 2.5 V
Length of tube = 0.35 m
We need to calculate the area of cross section
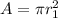
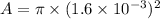
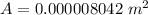
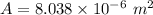
We need to calculate the resistance
Using formula of resistivity
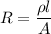
Put the value into the formula
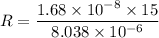
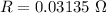
We need to calculate the current
Using formula of current
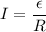
Where,
 = emf
= emf
Put the value into the formula
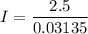
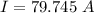
We need to calculate the number of turns per unit length
Using formula of number of turns
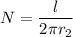
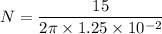
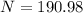
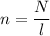
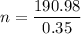
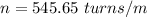
We need to calculate the magnetic field
Using formula of magnetic field
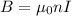
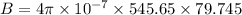
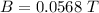
Hence, The magnitude of the magnetic field through the center of this solenoid is 0.0568 T.