Question

Eliminate the parameter in the parametric equations x =4 + sine t, y=6 + sine t, for 0≤t ≤pi/2 , and describe the curve, indicating its positive orientation. How does this curve differ from the curve x=4 + sine t, y= 6 + sine t, for pi/2 ≤t ≤pi ?

Answer 1

It is given that

`x=4+sin(t)....(i)\\y=6+sin(t)....(ii)`

Subtracting both the above equations we get

`x-y=-2\\\\\therefore x-y+2=0`

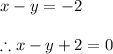
It is equation of a straight line.

The curve is drawn in the attached figure.

c)

The first curve is defined for 'x' ranging from 4 to 5 and 'y' ranging from 6 to 7 while as

The second curve is defined for 'x' ranging from 5 to 4 and 'y' ranging from 7 to 6

Since range and domain of both the curves is same thus they represent the same region.