Question

The population of a colony of mosquitoes obeys the law of uninhibited growth. If there are 1000 mosquitoes initially and there are 1300 after 1​ day, what is the size of the colony after 4 ​days?

Answer 1

2,855 is the size of the colony of mosquitoes after 4 ​days.

Step-by-step explanation:

The law of uninhibited growth is given as:

`A=A_o* e^(k* t)`

`A_o`= Original amount

A = Amount after time t

k = Positive constant repressing the rate of growth

We are given with:

Original population of mosquitoes = 1000

Population of mosquitoes after 1 day =1300

t = 1 day

`1300=1000* e^(k* 1 day)`

`k = 0.2623 day^(-1)`

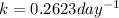
Population size of mosquitoes after 4 days

`A_o=1000, k= 0.2623 day^(-1)`

A =? , t = 4 days

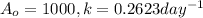
`A=1000* e^{ 0.2623 day^(-1)* 4 days}`

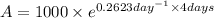
A =2,855.36 ≈ 2,855 mosquitoes

2,855 is the size of the colony of mosquitoes after 4 ​days.

Answer 2

`2855`

Step-by-step explanation:

As per the law of uninhibited growth

Population after a time period of "t" will be given by

`P(t)= P_0e^(kt)`

where,

`P_0` is the initial population.

k is the growth rate

Growth rate of mosquitoes

`1300= 1000*e^(k*1)\\e = 0.2623`per day

So, population of mosquitoes after four days will be

`= 1000* e^(0.2623*4)\\=1000*2.855 \\= 2855`