Question

The half-life of a positron is very short. It reacts with an electron, and the masses of both are converted to two gamma-ray photons. e+10 +0−1e⟶2???? This reaction is called an annihilation reaction. The mass of an electron or positron is 9.109×10−31 kg. (a) Calculate the energy produced by the reaction between one electron and one positron. (b) Assuming that the two γ-ray photons have the same frequency, calculate this frequency. J ????photon= Hz

Answer 1

Step-by-step explanation:

(a) It is known that relation between energy and mass is as follows.

`E = 2 * mc^(2)`

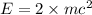
where, E = energy

m = mass

c = speed of light =
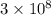`3 * 10^(8)` m/s

As it is given that mass is
`9.109 * 10^(-31)` kg. So, putting the given values into the above formula as follows.

`E = 2 * mc^(2)`

=
`2 * 9.109 * 10^(-31) kg * 3 * 10^(8)m/s`

=
`1.638 * 10^(-13) J`

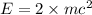
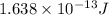
Therefore, we can conclude that the energy produced by the reaction between one electron and one positron is
`1.638 * 10^(-13) J`.

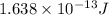(b) When gamma ray photons are produced then they will have the same frequency. Relation between energy and frequency is as follows.

E =
`h * \\u` ..... (1)

where, h = plank's constant =
`6.626 * 10^(-34) J.s`

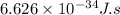
`\\u` = frequency

Also,
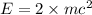`E = 2 * mc^(2)` ........ (2)

Hence, equating equations (1) and (2) as follows.

`h * \\u` =
`2 * mc^(2)`

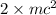
So,

`6.626 * 10^(-34) Js * \\u` =
`1.638 * 10^(-13) J`

`\\u` =
`1.236 * 10^(20) Hz`

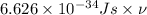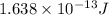
Thus, we can conclude that the frequency is
`1.236 * 10^(20) Hz`.