Question

A block is projected up a frictionless inclined plane with initial speed v0 = 6.48 m/s. The angle of incline is θ = 27.3. (a) How far up the plane does it go? (b) How long does it take to get there? (c) What is its speed when it gets back to the bottom?

Answer 1

distance = 4.67 m

time = 1.44s

speed = 6.48 m/s

Explanation:

initial speed v₀ = 6.48 m/s

θ = 27.3⁰

a) distance traveled by the block

`L = (v^2)/(2gsin \theta)\\L = (6.48^2)/(2* 9.8* sin 27.3^(o))\\L = 4.67 m`

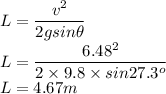
b) time taken to travel

`t = \sqrt{(2L)/(gsin\theta)}\\ t = \sqrt{(2* 4.67)/(9.8 * sin27.3^o)}\\t = 1.44s`

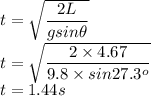
c) speed at the bottom

h = L sinθ

h = 4.67× sin 27.3°

h = 2.14 m

by law of conservation of energy

`mgh = (1)/(2)mv^2\\v = \sqrt{{2gh} } \\v = \sqrt{{2* 9.8*2.14} }\\v = 6.48 m/s`

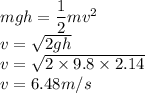
speed equal to 6.48 m/s