Question

Two teams of nine members each engage in a tug of war. Each of the first team's members has an average mass of 73 kg and exerts an average force of 1350 N horizontally. Each of the second team's members has an average mass of 78 kg and exerts an average force of 1358 N horizontally. (a) What is magnitude of the acceleration of the two teams, and which team wins? (b) What is the tension in the section of rope between the teams?

Answer 1

a = 0.052 m s^{-2}

T = 12185.49 N

Step-by-step explanation:

from the figure:

determine the Force
`F_R = NF_2i = 9*1358 i = 12222 N`

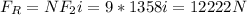
Determine the force
`F_L = NF_1i = 9*1350 i = - 12150ii N`

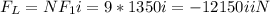
by Newton's second law, net force F_net

`F_net = \sum{F_1+ F_2 +...... = ma ........(1)`

`F_R +F_L = ma`

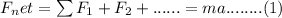
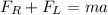
12222- 12150 = ma

`a = ( 72)/(9(78+73))`

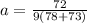
a = 0.052 m s^{-2}

B) TENSION T in section of rope

by newton's second law

`F_Ri -Ti = 9m_2ai`

`T = F_Ri - 9m_2ai`

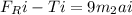
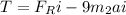
T = 12222i - 9*78*0.052

T = 12185.49 N