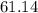Answer:
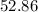 to
to
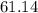
Explanation:
Data : 70, 45, 55, 60, 65, 55, 55, 60, 50, 55.
Sample mean =
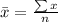
Sample mean =
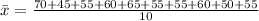
Sample mean =
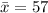
Sample standard deviation =
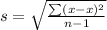
Sample standard deviation =
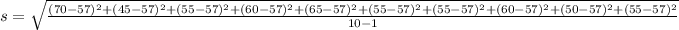
Sample standard deviation =
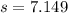
Since n < 30 and population standard deviation is unknown
So we will use t dist.
Confidence interval = 90%
So, significance level =α= 0.1
Degree of freedom = n-1 = 10-1 =9
Now refer the t dist table for t critical
So,

Formula of confidence interval =

Substitute the values
Confidence interval =
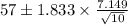
Confidence interval =
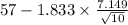 to
to
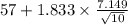
Confidence interval =
 to
to

Hence a 90% confidence interval for the population average length of time, in hours, for all engineers at start- ups work per week is
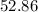 to
to