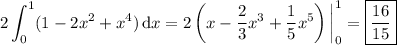Each cross section has a side length equal to the distance (parallel to the
 -axis) between the curves
-axis) between the curves
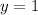 and
and
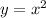 , which is
, which is
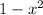 , and hence area of
, and hence area of
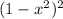 . The two curves intersect at
. The two curves intersect at
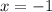 and
and
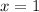 . Then the volume is equal to the integral
. Then the volume is equal to the integral
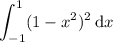
The integrand is even, since
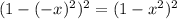
so we can make use of symmetry to simplify this to
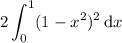
Computing the integral is trivial: