Answer:
63°.
Explanation:
To find the angle we can use as limits of the figure the intersection of y = 2x-4 with the x-axis and any point at the right of it.
To find the intersection of y = 2x-4 with the x-axis we do y=0:
0 = 2x-4
4 = 2x
x = 4/2 = 2.
Then, the left limit is (2,0). Now, let's use x=3 as an example to find the right limit:
y = 2(3)-4
y = 6-4
y = 2.
Then, the right limit is (3,2). You can see it in graph below. As you can see, the acute angle
 we are searching for can be calculated with the horizontal and vertical distances of the triangle limited by the two points, the line and the x-axis. So,
we are searching for can be calculated with the horizontal and vertical distances of the triangle limited by the two points, the line and the x-axis. So,
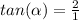
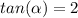
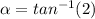
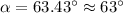 .
.