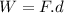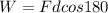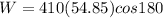Answer:
Part a)
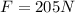
Part b)
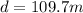
Part c)

Part d)

Part e)

Part f)

Step-by-step explanation:
Part a)
Mass of the rider = 50 kg
rate of deceleration of the object = 4.1 m/s/s
now we know by Newton's II law
F = m a
we have

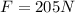
Part b)
Since the rider is decelerated then let say it will be stopped after moving distance "d"
then we have
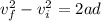
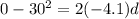
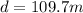
Part c)
Work done to stop the rider
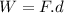
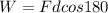
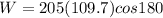

Part d)
Mass of the rider = 50 kg
rate of deceleration of the object = 8.2 m/s/s
now we know by Newton's II law
F = m a
we have
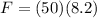

Part e)
Since the rider is decelerated then let say it will be stopped after moving distance "d"
then we have
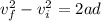


Part f)
Work done to stop the rider