Answer: 2.68
Explanation:
Given : Sample size :
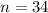
Mean :
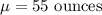
Standard deviation :
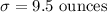
Significance level :
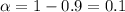
Critical value :
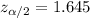
Formula for margin of error :-
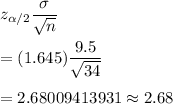
Hence, the maximal margin of error associated with a 90% confidence interval for the true population mean turtle weight. =2.68