Answer:
dimension of the rectangular tank = (20 ft × 20 ft × 10 ft)
Step-by-step explanation:
volume of rectangle = 4000 ft³
volume of the tank = a² × h
surface area of the tank = 4 × a × h + a²
from the volume of the tank h = 4000/a²
now surface area becomes
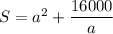
now ,
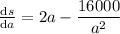
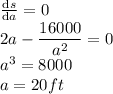
h = 10 ft.
hence, the dimension of the rectangular tank comes out to be
(20 ft × 20 ft × 10 ft)