Answer : The correct option is, (A) 0.081 mol/L
Explanation : Given,
Equilibrium constant = 18.0
Initial concentration of
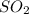 =
=
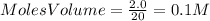
Initial concentration of
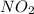 =
=
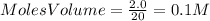
The balanced equilibrium reaction is,
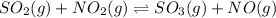
Initial conc. 0.1 0.1 0 0
At eqm. (0.1-x) (0.1-x) x x
The expression of equilibrium constant for the reaction will be:
![K_c=([SO_3][NO])/([SO_2][NO_2])](https://img.qammunity.org/2020/formulas/chemistry/high-school/uexkzvkxfgt26t5bb4ovbb4svbnjd2ulwy.png)
Now put all the values in this expression, we get :
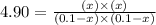
By solving the term 'x' by quadratic equation, we get two value of 'x'.
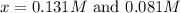
From this we conclude that, the value of x = 0.131 at equilibrium can not be more than the initial concentration. So, the value of 'x' which is equal to 0.131 M is not consider.
The concentration of
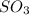 at equilibrium = x = 0.081 M
at equilibrium = x = 0.081 M
Therefore, the concentration of
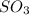 at equilibrium is, 0.081 M
at equilibrium is, 0.081 M