Question

A 2 kg ball is attached by a string to the top of a vertical pole and swings in a circle of radius 1.2 m. If the string makes and angle of 18° with the pole, how fast is the ball moving?

Answer 1

v = 3.81 m/s

Step-by-step explanation:

First, we will find out the radius (r)

sinΘ = r / L

or

r = LsinΘ

on substituting the values, we get

r = 1.2 × sin18°

or

r = 0.370 m

Now,

The tension (T) can be calculated as

ΣF(y) = 0

or

Tcos18° - mg = 0

or

T = mg / cos18.8°

on substituting the values, we have

T = (2kg x 9.8m/s²) / cos18°

or

T = 20.60 N

Now, applying the equilibrium condition in horizontal direction. we have

`\Sigma F_x = ma_c = Tsin\theta = 0`

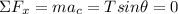
also, the centripetal acceleration
`a_c=(v)/(r)`

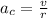
on substituting the values, we get

m(v² / r) = Tsin18°

v = (rTsin18° / m)

v = [(1.2m)(20.60 × sin18°) / 2kg]

v = 3.81 m/s