Question

Speakers A and B are vibrating in phase. They are directly facing each other, are 7.80 m apart, and are each playing a 73.0 - Hz tone. The speed of sound is 343 m/s. One the line between the speakers there are three points where constructive interference occurs. What are the distances of these three points from speaker A?

Answer 1

x = 6.25 m , x = 3.90 m , x = 1.55 m

Step-by-step explanation:

given,

frequency of tone = 73 Hz

speed of sound = 343 m/s

distance between the speaker = 7.80 m

wavelength (λ) =
`(v)/(\mu)`

=
`(343)/(73)`

= 4.7 m

let the distance from speaker A be x

distance from speaker B be 7.80 - x

distance of the first point from speaker A

x - (7.80 - x) = one wavelength

2x - 7.80 = 4.7

x = 6.25 m

distance of the second point from speaker A

x - (7.80 - x) = zero wavelength

2x - 7.80 = 0

x = 3.90 m

distance of the second point from speaker A

(7.80 -x) - x = one wavelength

7.80 - 2x = 4.7

x = 1.55 m

Answer 2

The distances of these three points from speaker A are 6.25 m, 3.9 m and 1.55 m.

Step-by-step explanation:

Given that,

Distance = 7.80 m

Frequency f = 73.0 Hz

Speed of sound = 343 m/s

We need to calculate the wavelength

Using formula of wavelength

`\lambda=(v)/(f)`

Put the value into the formula

`\lambda=(343)/(73.0)`

`\lambda=4.6986\ m`

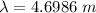
Let the distance from speaker A is x.

The distance from speaker B is (7.80-x).

Difference between the distance must be a whole number of wavelength.

For first point,

`x-(7.80-x)= \lambda`

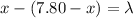
Put the value of wavelength

`2x-7.80=4.6986`

`2x=4.6986+7.80`

`x=(12.4986)/(2)`

`x=6.25\ m`

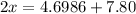
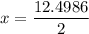
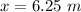
For second point,

`x-(7.80-x)= \lambda`

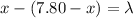
Put the value of wavelength

`2x-7.80=0`

`x=3.9\ m`

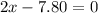
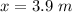
For third point,

`(7.80-x)-x= \lambda`

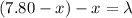
Put the value of wavelength

`7.80-2x=4.6986`

`-2x=4.6986-7.80`

`2x=3.1014`

`x=(3.1014)/(2)`

`x=1.55\ m`

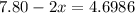
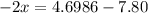
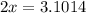
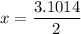
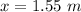
Hence, The distances of these three points from speaker A are 6.25 m, 3.9 m and 1.55 m.