Answer:
Givens:
We know that kinetic energy is:
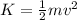
So, we just need to calculate the speed. We have the equation of the movement, if we derivate that expression, we'll have the speed:
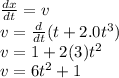
Which is the speed at any time t.
Now, we replace the expression to find the kinetic energy at any time t:
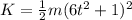

So, this is the kinetic energy at energy at any time t.
Through derivation we can find the acceleration and force at any time t:
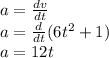
Also, we know that

Replacing values:

The power is define as the product of the force and the velocity:

At last, we now that the work is define as:
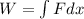
So, we just replace the force, and integrate it between t=0 and t=2 sec.
![W=\int _(0)^(2) 48t(6t^(2)+1)dt\\W=\int_(0)^(2) (288t^(3)+48t)dt\\W= (288t^(4) )/(4)+(48t^(2))/(2) ]_(0)^(2) \\W= 72t^(4)+24t^(2)]_(0)^(2)\\W=72(2)^(4)+24(2)^(2)\\W= 1152 + 96=1248 \ J](https://img.qammunity.org/2020/formulas/physics/college/omnn60b9247ss5f88aa42wpwis2roaj8x7.png)