Answer:
The system has infinitely solutions
Explanation:
The system shown in the attached picture can be simplify by performing natural divisions
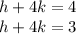
Since the equations are equal in terms, we have a system where one equation is a contradiction of the other
On one side it says h+4k=4 and the other says h+4k=3
This system has more variables than equations, it has infinitely solutions