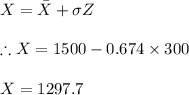Question

Scores on the SAT are normally distributed with a mean of 1,500 and a standard deviation of 300. a. What percent of scores are greater than 1750? b. What percent of scores are less than 1150? c. What percent of scores are between 1400 and 1800? d. What score would put an applicant in the top 10 percent? e. What score would put an applicant in the bottom 25 percent?

Answer 1

It is given that

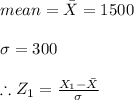
`mean=\bar{X}=1500\\\\\sigma =300\\\\\therefore Z_(1)=\frac{X_(1)-\bar{X}}{\sigma }`

for
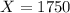`X=1750` we have

`\therefore Z_(1)=(1750-1500)/(300 )=0.833`

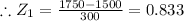
using the standard normal distribution table we have area above
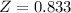`Z=0.833` equals
`20.23%`

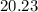
b)

Similarly for scores less than 1150 we have

`\therefore Z_(2)=(1150-1500)/(300 )=-1.16`

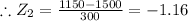
using the standard normal distribution table we have area below
`Z=-1.16` equals
`12.17%`

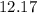
c)

The score that would put the applicant in top 10% shall correspond score whose value gives 90% area of the normal distribution graph

For area of 90% we have Z=1.281

Thus we have

`X=\bar{X }+\sigma Z\\\\\therefore X=1500+1.281* 300\\\\X=1884.4`

d)

The score that would put the applicant in bottom 25% shall correspond score whose value gives 25% area of the normal distribution graph

For area of 25% we have Z=-0.674

Thus we have

`X=\bar{X }+\sigma Z\\\\\therefore X=1500-0.674* 300\\\\X=1297.7`