Answer:
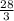
Explanation:
Given information: ABCD is a rectangle,
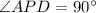 , PA=20, AQ=25 and QP=15.
, PA=20, AQ=25 and QP=15.
In a right angled triangle
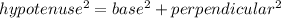
In triangle ABP, AB = 16 and AP = 20. Using Pythagoras theorem we get
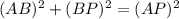
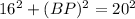
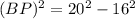
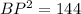
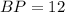
Since BP = PT, therefore PT = 12.
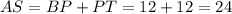
AQS is a right angled triangle and AQ = 25. Use Pythagoras theorem in triangle AQS.
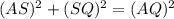
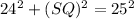
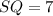
Triangle PQT is a right triangle. Use Pythagoras theorem in triangle PQT.
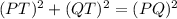
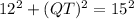
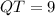
In triangle PTQ and DSQ,
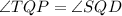 (Vertical angles)
(Vertical angles)
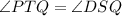 (Right angles)
(Right angles)
Triangle PTQ is similar to triangle DSQ by AA property of similarity.
Corresponding parts of similar triangles are proportional.
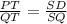
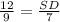
On cross multiplication we get
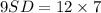
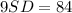
Divide both sides by 9.
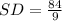
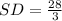
Therefore,
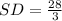 .
.