Question

Momentum: A satellite, initially at rest in deep space, separates into two pieces, which move away from each other. One piece has a mass of 190 kg and moves away with a speed 0.280 c, and the second piece moves in the opposite direction with a speed 0.600 c. What is the mass of the second piece?

Answer 1

m = 73.88 kg

Step-by-step explanation:

total momentum = 0

P_1 +P_2 = 0

P_1 =P_2

WE KNOW THAT MOMENTUM IS GIVEN BY:

`P_1 =\frac{mv_1}{\sqrt{1 -(v_1^2)/(c^2)}} </p><p> [tex] =\frac{190*.280}{\sqrt{1 -(0.280^2)/(c^2)}}`

= 55.41c

second momentum with light velocity

`P_2 =- P_1`

`\frac{mv_2}{\sqrt{1 -(v_2^2)/(c^2)}} = 55.41c`

`mv_2 =5541c *\sqrt{1 -(v_2^2)/(c^2)`

`m *0.600c = 55.41c *\sqrt{1 -(0.600^2)/(c^2)`

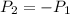
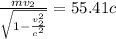
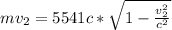
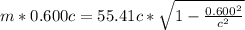
solving for m we get

m = - 73.88 kg

-ve show that second mass moves in opposite direction to first mass.