Step-by-step explanation:
It is given that,
Slit width,
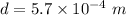
A diffraction pattern is formed on a flat screen located 4.0 m away, L = 4 m
The distance between the middle of the central bright fringe and the first dark fringe is 4.2 mm, y = 4.2 mm = 0.0042 m
Let
 is the wavelength of the light.
is the wavelength of the light.
Using condition of diffraction as,

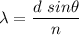 ..............(1)
..............(1)
Also,
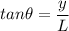
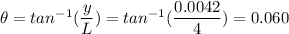
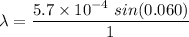
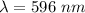
So, the wavelength of the light is 596 nm. Hence, this is the required solution.