Question

In a survey of 1072 ​people, 788 people said they voted in a recent presidential election. Voting records show that 71​% of eligible voters actually did vote. Given that 71​% of eligible voters actually did​ vote, (a) find the probability that among 1072 randomly selected​ voters, at least 788 actually did vote.​ (b) What do the results from part​ (a) suggest?

Answer 1

p(x >788) = 0.0351

voted voters may be less than 788

Explanation:

given data:

n =1072

p = 0.71

`\mu =n*p = 1072*0.71 = 761.12`

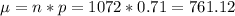
nq = 1072*0.29 = 310.88

using below relation

`\sigma = √(n*p*(1-p)) = 14.85`

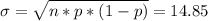
as np and nq > 5, thus we can use normal approximation to binomial distribution i.e.

p(x >788) = 1 - p(x <788)

`= 1 - p( (x -\mu)/(\sigma)) < ((788 - 761.12)/(14.85))`

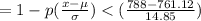
= 1 - p (z <1.81)

= 1 - 0.9649 { from z tables}

p(x >788) = 0.0351

b)This suggest that there is very less chance that among 1072 randomly selected​ voters, at least 788 actually did vote. Actually voted voters may be less than 788