Answer:
The area between the circles grow at 192%.
Explanation:
Consider the provided information.
There are two concentric circles with radii 10 and 8.
Area between the two circles = π×10²−π×8²
π×(10²−8²)=π×(100-64)
π×(36)=36π
If the radius of the outer circle is increased by 10% and the radius of the inner circle decreased by 50%,
10% of 10 is 1. Thus the new radius of bigger circle is 10+1=11.
50% of 8 is 4. Thus the new radius of the smaller circle is 8-4=4.
Area between the two circles upon change in Radii is
π×(11²−4²)=π×105
Change in area is 105π-36π = 69π
%change in Area=(Change in Area/Original Area)×100
Substitute the respective values in the above formula.

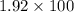

Hence, the area between the circles grow at 192%.