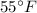Answer:
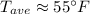
Explanation:
Given :
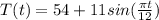
To Find : Find the average temperature Tave during the period from 9 AM to 9 PM.
Solution:
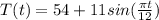
Where t is hours after 9 AM
Now we are supposed to find the average temperature Tave during the period from 9 AM to 9 PM
Period : 9 a.m. to 9 p.m.
Hours between 9 am to 9 pm = 12
Interval of function: [0,12]
So, we will use mean value theorem
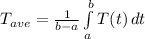
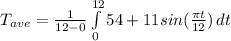
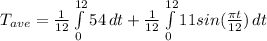
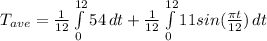
let
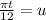
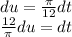
u(0)=0
u(12)=π
Now apply this substitution on right integral
![T_(ave)=(1)/(12)[54t]^(12) _0+(1)/(12) *(12)/(\pi)* 11 \int\limits^(\pi)_0{ sin u} \, du](https://img.qammunity.org/2020/formulas/mathematics/college/lnm9fwdlho600pbvwbt1lejo1t0dyscfhl.png)
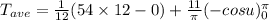
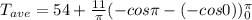
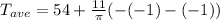
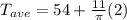
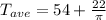
So,
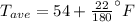
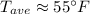
Hence the average temperature Tave during the period from 9 AM to 9 PM is