Question

PLEASE HELP URGENT EXPLAIN HOW TO DETERMINE IF ITS INCREASING OR DECREASING

Answer 1

Decreasing from 0 to infinity.

Explanation:

Write the function:

`h(x)=-5√(x)`

If you look and analyze the function, we already can tell that it doesn't admit negative numbers, because you can't take the square root of a negative number. Theferore, all the options that go from -∞ to 0 are not correct, because the function doesn't even generate values in that interval.

Then, to see of the function increases or decreases from 0 to ∞, just evaluate the function, at least 3 times, to see where the values of y go.

Let's take 3 arbitrary values for this:

`h(0)=-5√(0) =0\\\\h(0)=-5√(49) =-35\\\\h(0)=-5√(15000) =-612.372\\`

With these values, we can clearly tell that the function is decreasing from 0 to infinity.

A more analytic way to determine this would be by finding the average rate of change of the function on an interval that goes from 0 to any number but infinity.

Average rate of change formula:
`A(x)=(h(b)-h(a))/(b-a)`

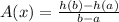
Take arbitrary values and substitute the function:

`A(x)=(h(50)-h(5))/(50-5)\\\\A(x)=(-35.35-(-11.18))/(45)\\\\A(x)=(-35.35+11.18)/(45)\\\\A(x)=(-24.17)/(45)\\\\A(x)= -0.5364`

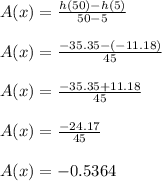
The result is -0.5364, this means that the average change or the function from x=5 to x=50 is negative, and this indicates that the function is decreasing.

Answer 2

The function is decreasing on the interval (0, ∞).

Explanation:

Definitions

• Domain: Set of all possible input values (x-values).
• A function is said to be increasing if the y-values increase as the x-values increase.
• A function is said to be decreasing if the y-values decrease as the x-values increase.

Given function:

`h(x)=-5√(x)`

The parent function of the given function is:

`y = √(x)`

As we cannot square root a negative number, the parent function has a restricted domain of [0, ∞).

As
`√(x)\geq 0` the parent function is increasing on the interval (0, ∞).

Transformations

`y=a\:f(x) \implies f(x) \: \textsf{stretched parallel to the y-axis (vertically) by a factor of}\:a`

`y=-f(x) \implies f(x) \: \textsf{reflected in the} \: x \textsf{-axis}`

Therefore, the parent function has been stretched vertically by a factor of 5 and reflected in the x-axis to become function h(x).

Therefore, the domain remains the same.

The stretch does not affect the increasing/decreasing nature of the function, but as the function is reflected in the x-axis, it is now decreasing on the interval (0, ∞).